ESSA PÁGINA ESTÁ EM CONSTRUÇÃO. SE TIVER DÚVIDAS OU ENCONTRAR ALGUM ERRO, DEIXE UM COMENTÁRIO.
OBRIGADO. :)
1) (2015 - UNA) Uma taça será fabricada em formato de um cone e terá 16cm de diâmetro e altura correspondente ao triplo do raio. Qual será a capacidade desta taça? (Utilize π = 3,14).
A) 1.607,68cm³
B) 1.903cm³
C) 2.340,87cm³
D) 1.250,92cm³
O raio corresponde à metade do diâmetro de um círculo. Então, o raio terá 8cm.
A altura do cone corresponde ao triplo do raio, ou seja, 24 cm.
O volume de um cone é dado pela fórmula:
[tex]V_{Cone} = \frac{\textrm{Área do círculo} * \textrm{Altura}}{3}[/tex]
[tex]V_{Cone} = \frac{(r^{2}\pi) * 24}{3}[/tex]
[tex]V_{Cone} = 8^{3}*\pi [/tex]
[tex]V_{Cone} = 512 * 3,14[/tex]
[tex]V_{Cone} = 1607,68[/tex]
Letra A.
2) (2014 - FAFIPA) Um retângulo possui 20 cm de comprimento e 6 cm de altura. Qual é o seu perímetro?
A) 52 cm
B) 54 cm
C) 86 cm
D) 120 cm
Perímetro do retângulo = 2 * (comprimento + altura)
Perímetro do retângulo = 2 * (20 + 6)
Perímetro do retângulo = 2 * (26)
Perímetro do retângulo = 52
3) (2014 - IDECAN) A seguir estão representados um triângulo equilátero e um quadrado, cujos perímetros são iguais.

Se a diferença entre os lados dessas 2 figuras é igual a 3 cm, então, o perímetro de cada uma delas mede
A) 24 cm.
B) 28 cm.
C) 32 cm.
D) 36 cm.
E) 40 cm.
O perímetro do triângulo = 3 * LadoT
O perímetro do quadrado = 4 * LadoQ
O enunciado informa que a diferença entre os lados dessas figures é igual a 3 centímetro. Como o triângulo tem lados mais compridos, segue que:
LadoT = LadoQ + 3
Perímetro do quadrado = Perímetro do triângulo
4 * LadoQ = 3 * LadoT
4 * LadoQ = 3 * (LadoQ + 3)
4 * Lado Q = 3 * LadoQ + 9
(4 * Lado Q) - (3 * LadoQ) = 9
LadoQ = 9
LadoT = 12
Perímetro do Quadrado = 4 * 9 = 36 cm
Perímetro do Triângulo = 3 * 12 = 36 cm
Letra D.
4) (2013 - CESPE) Considerando que as retas [tex]R_{1}[/tex], [tex]R_{2}[/tex], [tex]R_{3}[/tex] e [tex]R_{4}[/tex] sejam distintas e estejam no mesmo plano, e que, se a reta [tex]R_{i}[/tex] intercepta a reta [tex]R_{j}[/tex], [tex]P_{ij}[/tex] — em que i, j = 0, 1, 2, 3, 4 e i ≠ j — denote o ponto de interseção dessas retas, julgue o item seguinte.
Se os pontos [tex]P_{12}[/tex], [tex]P_{13}[/tex] e [tex]P_{23}[/tex] existirem e forem distintos, então a reta R1 não poderá ser perpendicular à reta R2.
O ponto [tex]P_{12}[/tex] é o ponto em que as retas [tex]R_{1}[/tex] e [tex]R_{2}[/tex] se interceptam.
O ponto [tex]P_{13}[/tex] é o ponto em que as retas [tex]R_{1}[/tex] e [tex]R_{3}[/tex] se interceptam.
O ponto [tex]P_{23}[/tex] é o ponto em que as retas [tex]R_{2}[/tex] e [tex]R_{3}[/tex] se interceptam.
As retas são distintas e estão no mesmo plano, os três pontos também são distintos. Segue que as três retas formam um triângulo. Não há nada que impeça de ser um triângulo retângulo, então a assertiva está errada.
5) (2013 - CESPE) No caso de os pontos P12, P13 e P14 existirem e P12 = P13 = P14, então os pontos P34 e P23 também existirão e P34 = P23.
Sim, se a reta [tex]R_{1}[/tex] cruza as retas [tex]R_{2}[/tex], [tex]R_{3}[/tex] e [tex]R_{4}[/tex] no mesmo ponto, segue que as 4 retas passam pelo ponto [tex]P_{12}[/tex]. Portanto, todas as retas se encontram no mesmo ponto e [tex]P_{12}[/tex]=[tex]P_{34}[/tex]=[tex]P_{23}[/tex].
6) (2014 - CESGRANRIO) Três herdeiros, Arnaldo, Bruno e Paulo, dividiram um terreno quadrado de 42 metros de lado em três terrenos retangulares de áreas iguais. A Figura abaixo mostra a divisão e a parte que coube a cada um.

O perímetro, em metros, do terreno retangular destinado a Bruno é
A) 105.
B) 112.
C) 126.
D) 147.
E) 588.
O terreno tem 42 metros de lado.
O terreno tem 42² metros de área, isto é, 1.764 m².
Cada herdeiro ficou com 1/3 da área ou 588 m².
Os terrenos de Arnaldo e de Paulo possuem o mesmo comprimento e área e, portanto, possuem também a mesma altura.
Altura do terreno de Arnaldo + Altura do terreno de Paulo = 42 metros.
Segue que a altura desses terrenos mede 21 m.
Se a área é de 588m² e a altura é de 21m, o comprimento é igual 588 / 21 = 28 m.
O terreno de Bruno tem 14 metros de comprimento.
O perímetro do terreno de Bruno é igual a 2 * (42 + 14) = 112 m.
7) (2012 - CESGRANRIO) Um “elevador”, especificamente construído para tal prédio, se deslocará sobre as arestas, ao receber ordens dos seus passageiros, como: “para cima” e “para baixo” (na orientação indicada na figura), “para direita” e “para a esquerda” (na orientação dos passageiros do elevador que estão voltados de frente para o centro geométrico do cubo). Ao receber uma ordem, o elevador se deslocará sobre a aresta que viabiliza o sentido do movimento ordenado e parará ao alcançar um vértice, aguardando uma nova ordem.

Se o elevador estiver inicialmente sobre o vértice D e receber as ordens “para a direita”, “para cima”, “para a esquerda”, “para a esquerda”, “para baixo”, “para direita”, “para direita” e “para a direita”, ele não passará pelo vértice:
A) A
B) B
C) C
D) F
E) G
Para funcionar, os passageiros devem permanecer voltados de frente para o centro do elevador independentemente do vértice em que se encontram. Partindo do vértice D, o elevador fez a seguinte trajetória.

Se mantivermos o ponto de vista dos passageiros fixo e igual ao inicial, o elevador faria uma trajetória que não passaria pelo vértice H. Ainda bem que não há essa resposta disponível.
8) (2015 - UTFPR) Uma pessoa deseja cobrir o piso e as paredes de um banheiro retangular com revestimento cerâmico. As dimensões do banheiro são: 1,70 metros(m) de largura por 2,50m de comprimento por 2,40m de altura. Nesse banheiro, há uma porta de 0,60 m de largura por 2,10m de altura e uma janela de 1,20m de comprimento por 0,60m de altura. Considera-se, inicialmente, uma perda de no máximo 10% de material. Os revestimentos cerâmicos são vendidos em caixas que contém 2,14 metros quadrados (m²). Assinale a alternativa que apresenta o número de caixas desses revestimentos que deverão ser compradas para cobrir o piso e as paredes desse banheiro.
Observação: os revestimentos que sobrarem serão guardados, para eventuais futuras reposições, no piso ou nas paredes.
A) 2 ou 3 caixas para o piso e 9 ou 10 caixas para as paredes.
B) 3 ou 4 caixas para o piso e 11 caixas para as paredes.
C) 2 caixas para o piso e 11 ou 12 caixas para as paredes.
D) 3 ou 4 caixas para o piso e 12 caixas para as paredes.
E) 2 ou 3 caixas para o piso e 8 caixas para as paredes.
O banheiro é composto por duas duplas de paredes distintas e um piso que devem ser revestidos.
Área da parede A = largura * altura = 1,7 * 2,4 = 4,08 m²
Área da parede B = comprimento * altura = 2,5 * 2,4 = 6 m²
Área da piso = largura * comprimento = 1,7 * 2,5 = 4,25 m²
Área da porta = 0,6 * 2,1 = 1,26 m²
Área da janela = 1,2 * 0,6 = 0,72 m²
Área das paredes = 4,08 + 4,08 + 6 + 6 = 20,16 m²
Área da porta e janela = 1,26 + 0,72 = 1,98 m²
Área das paredes que deve ser revestida = 20,16 - 1,98 = 18,18 m²
Com 10% de perda do material, cada caixa cobre em média uma área de 1,926 m²
Número de caixas para preencher as paredes = 18,18 / 1,926 = 9,42 caixas
número de caixas para o piso = 4,25 / 1,926 = 2,2 caixas
É necessário arredondar para cima. Será necessárias 12 caixas para preencher todo o espaço, sendo que pode-se usar 10 caixas para as paredes e o que restar da décima será usado em complemento com as 2 caixas destinadas ao piso. Pode-se também usar 3 caixas para o piso, e o restante da terceira caixa é usado em complemento com 9 caixas destinadas às paredes.
Letra A.
9) (2011 - FDC) A medida da diagonal de uma caixa cúbica é igual a [tex]4\sqrt{3}[/tex] m. O volume, em m³, ocupado por essa caixa é igual a:
A) 64
B) 32
C) 24
D) 16
E) 12
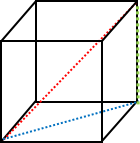
Na imagem temos um cubo, a diagonal do cubo em vermelho, a diagonal do quadrado em azul e uma aresta em verde.
A medida da diagonal azul é igual a [tex]\sqrt{lado^{2} + lado^{2}}[/tex] pelo teorema de pitágoras. Vou chamar essa medida de X.
A medida da diagonal vermelha é igual a [tex]\sqrt{x^{2} + lado^{2}}[/tex] pelo teorema de pitágoras.
Ou seja, [tex]\sqrt{x^{2} + lado^{2}} = 4\sqrt{3}[/tex]
[tex]x^{2} + lado^{2} = (4\sqrt{3})^{2}[/tex]
[tex]x^{2} + lado^{2} = 16 * 3[/tex]
[tex]x^{2} + lado^{2} = 48[/tex]
[tex](\sqrt{lado^{2} + lado^{2}})^{2} + lado^{2} = 48[/tex]
[tex]lado^{2} + lado^{2} + lado^{2} = 48[/tex]
[tex]3*lado^{2} = 48[/tex]
[tex]lado^{2} = 16[/tex]
[tex]lado = 4[/tex]
[tex]Volume = lado^{3} = 64[/tex]
10) (2012 - CEC) Num recipiente em forma de cilindro circular reto, com raio de base 2cm e altura 6√3 cm (dimensões internas), há volume de água de 16π√3 cm³ (figura 1). Qual deve ser o maior ângulo α (figura 2) que o plano da base do cilindro deve fazer com o plano de apoio para que a água não se derrame ao se inclinar o cilindro?

A) 60º
B) 40º
C) 45º
D) 90º
E) 30º
Volume do cilindro = área da base vezes altura
Área da base (círculo) = r²π = 2²π = 4π
Volume cilindro = 4π * 6√3 = 24π√3 cm³
A água preenche 16π√3 cm³ do cilindro ou 2/3 da capacidade.
O cilindro está 1/3 vazio para os pessimistas, o que significa dizer 8π√3 cm³ vazio.
Na parte interna do cilindro em perspectiva ortográfica, haverá 3 figuras que se parecem com dois triângulos idênticos, [tex]Q_{1}[/tex] e [tex]Q_{2}[/tex], e um retângulo, P.

Apesar de não serem propriamente triângulos ou retângulo, isso não interessa, pois podemos calcular o volume das figuras do mesmo jeito. Afinal, já sabemos que o espaço vazio [tex]Q_{2}[/tex] representa 1/3 do volume do cilindro, ou seja, 8π√3 cm³.
Por semelhança, o "triângulo" [tex]Q_{1}[/tex] tem o mesmo volume, 8π√3 cm³.
Já que os dois triângulos representam 2/3 do volume do cilindro, o restante é explicado pelo volume do "retângulo".
O "retângulo" P é na verdade é um cilindro, com área da base circular igual a 4π e volume 8π√3.
Com essa informação é possível calcular a altura do cilindro P.
Altura de P = Volume / Área da base = 8π√3 / 4π = 2√3 cm.
Portanto, o "triângulo" [tex]Q_{1}[/tex] tem base igual 4√3 cm e altura igual a 4 cm (diâmetro da base circular do cilindro).

Usando o conhecimento de trigonometria, a tangente do ângulo β é a razão entre os lados opostos e adjacentes desse ângulo.
Tan(β) = Lado oposto / Lado Adjacente
Tan(β) = 4 / 4√3
Tan(β) = 1 / √3
β = 30°
Os ângulos α e β são complementares, significa dizer que α + β = 90°.
Conclui-se que α = 60°.
11) Na Figura abaixo, o quadrilátero ABCD é um quadrado de lado medindo 10 cm e o ponto O é centro de uma circunferência que possui os pontos A, B e E em comum com o quadrado. Nessas condições, é CORRETO afirmar que o comprimento da circunferência e o perímetro do quadrado, em centímetros, são, respectivamente, iguais a:

A) 12,5π e 40
B) 13,45π e 40
C) 16 e 12,5π
D) 14,5π e 16
Suponha que o centro da circunferência O coincida com a origem do plano cartesiano.
A equação do círculo é igual a [tex]y^{2}+x^{2}=r^{2}[/tex], em que r é o raio da circunferência.
O ponto E está localizado em (0, -r) no gráfico.
Como a distância EC é a metade da diastância BC, segue que [tex]y=2x-r[/tex] é a equação de uma reta que passa pelos pontos E e B. A inclinação da reta é 2, devido a relação entre EC e BC e a reta intercepta o eixo Y em -r.

Resolvendo o sistema de equações por meio de substituição da equação da reta na do círculo:
[tex]y^{2}+x^{2}=r^{2}[/tex]
[tex](2x-r)^{2} + x^{2} = r^{2}[/tex]
[tex]4x^{2}-4rx+r^{2}+x^{2}=r^{2}[/tex]
[tex]5x^{2}-4rx=0[/tex]
[tex]x(5x-4r)=0[/tex]
[tex]x=0[/tex] ou [tex]\frac{4r}{5}[/tex]
Note que x deve ser igual a 5 para que a aresta do quadrado seja igual a 10 cm.
Portanto, [tex]\frac{4r}{5}=5[/tex]
4r = 25
r = 25/4
r = 6,25 cm.
Perímetro do círculo = 12,5π cm.
Perímetro do quadrado = 40 cm.
Outra solução mais simples envolve aplicar a Teorema de Pitágoras no triângulo retângulo azul da imagem:

O lado do triâgulo é igual a metade da aresta do quadrado, 5 cm.
A altura do triângulo é igual à altura do quadrado subtraída pelo raio da circunferência, 10-r cm.
A hipotenusa do triângulo é igual ao raio da circunferência, r cm.
[tex](10-r)^{2}+5^{2}=r^{2}[/tex]
[tex]100-20r+r^{2}+25=r^{2}[/tex]
[tex]-20r+r^{2}-r^{2}=-100-25[/tex]
[tex]-20r=-125[/tex]
[tex]r=6,25[/tex] cm
12) (2013 - FGV) Consideremos cinco cidades A, B, C, D e E, e suas posições relativas descritas a seguir.
1. A cidade B está a 40 km da cidade A na direção nordeste.
2. A cidade C está a 40 km da cidade B na direção oeste.
3. A cidade D está a 40 km da cidade C na direção sul.
4. A cidade E está a 40 km da cidade D na direção leste.
Sejam w, x, y e z as distâncias da cidade A, respectivamente, às cidades B, C, D e E.
Então:
A) w = x = y = z.
B) w < x < y < z.
C) y < x = z < w.
D) y < w = x = z.
E) w = y < x = z.
As cidades estão localizadas no seguinte esquema:

As distâncias w, x, y e z podem ser representadas assim:

Note que o ângulo [tex]\angle ABC[/tex] tem 45º e que BC e CD têm 40 km. Segue que BCD forma um triângulo retângulo passando por A e portanto o ângulo [tex]\angle ADC[/tex] tem 45º também.

Como o ângulo [tex]\angle CDE[/tex] tem 90º e o ângulo [tex]\angle ACD[/tex] tem 45º, seguem que o ângulo [tex]\angle ADE[/tex] tem 45º. Os triângulos ACD e ADE compartilham o lado AD, os lados CD e DE possuem o mesmo comprimento. Dois triângulos que têm dois lados com o mesmo comprimento e um ângulo em comum são idênticos. Conclui-se que AC = AE, ou seja, x=z.

Pode-se afirmar que x e z são menores que w, já que w tem 40 km. A distância w é igual às distâncias dos segmentos CD e DE. Para que x fosse maior que CD, seria necessário que o ângulo [tex]\angle ACD[/tex] fosse obtuso (maior que 90º), mas não é o caso.
Pode-se também afirmar que x e z são maiores que y, pois o ângulo [tex]\angle ACD[/tex] tem menos que 45º graus.
Se quiser, é possível calcular o valor de y usando o Teorema de Pitágoras. A hipotenusa do triângulo BCD é igual a w+y. Então usando o Teoreama de Pitágoras:
BD² = BC² + CD²
(w + y)² = 40² + 40²
(40 + y)² = 1600 + 1600
1600 + 80y + y² = 3200
y² + 80y - 1600 = 0
Aplicando a fórmula de Bhaskara:
[tex]x_{1,2}=\frac{-80\pm \sqrt{80^{2}-4*1*(-1600)}}{2*1}[/tex]
[tex]x_{1,2}=\frac{-80\pm \sqrt{23900}}{2}[/tex]
[tex]x_{1}=40(-\sqrt{2}-1)[/tex] distância negativa pode ser descartada
[tex]x_{2}=40(\sqrt{2}-1)[/tex]
[tex]x_{2}\approx 16,57[/tex]
13) (2016 - Vunesp) Uma escola, com apenas um pavimento, está construída em um terreno retangular cuja lateral mede o triplo da medida de frente desse terreno. Sabendo-se que a área de toda a escola foi construída sobre uma base de concreto, também retangular, com exatamente 7500 metros quadrados, em que o maior lado media 60 metros a menos que o maior lado do terreno, e o menor lado media 20 metros a menos que o menor lado do terreno, a área total desse terreno, em metros quadrados, é:
A)14400.
B)14500.
C)14600.
D)14700.
E)14800.
Frente do terreno = F
Comprimento do terreno = 2F
Largura da escola = 3F - 60
Comprimento da escola = F - 20
Área da escola = 7.500 m²

Aplicando a fórmula da área do retângulo:
(3F - 60) * (F - 20) = 7500
3F² - 120F + 1200 = 7500
3F² - 120F - 6300 = 0
F² - 40F - 2100 = 0
(F + 30) (F - 70) = 0
F = -30 ou 70 m.
F = 70m
Área do terreno:
A = 3F * F
A = 3F²
A = 3(70²)
A = 3(4900)
A = 14.700 m²
14) (2016 - Vunesp) O formato interno de uma caixa d’água é um prisma triangular reto, cuja base é um triângulo retângulo com o maior lado medindo 2,5 metros, e o menor lado,1,5 metro. Se essa caixa comporta um volume máximo de água igual a 15000 litros, então é verdade que sua altura interna mede, em metros,
A) 10.
B) 8,5.
C) 7
D) 5,5.
E) 4.
Lado triângulo = L
1,5² + L² = 2,5²
L² = 2,5² - 1,5²
L² = 6,25 - 2,25
L² = 4
L = 2 m
Área do triângulo = (base * altura) / 2
Á = (2 * 1,5)/2
A = 1,5 m²
15.000 L = 15 m³
Volume do prisma = Área da base * altura do prisma
15 = 1,5 * altura
Altura do prisma = 10 m
15) (2012 - Quadrix) Uma pessoa tem 80m de arame para cercar um terreno de forma retangular, sendo que um dos lados do terreno é um rio que não precisará de cerca de arame. Qual deve ser o valor de cada lado X para que o terreno cercado tenha a máxima área?

A) 20 m
B) 25 m
C) 18 m
D) 28 m
Considerando que a largura da cerca igual a x e que o comprimento igual a y.
O perímetro da cerca será 2x + y = 80.
A área será igual a x * y.
A forma mais elementar de resolver é testando as alternativas.
A) 2x + y = 80
2(20) + y = 80
40 + y = 80
y = 40
Área = 20 x 40 = 800 m²
B) 2x + y = 80
2(25) + y = 80
50 + y = 80
y = 30
Área = 25 x 30 = 750 m²
C) 2x + y = 80
2(18) + y = 80
36 + y = 80
y = 44
Área = 18 x 44 = 792 m²
D) 2x + y = 80
2(28) + y = 80
56 + y = 80
y = 24
Área = 28 x 24 = 672 m²
A letra A obteve a maior área.
Se quiser resolver de forma mais matemática, pode-se proceder primeiro reescrevendo a função da área com respeito a x. Partindo da fórmula do perímetro,
2x + y = 80
y = 80 - 2x
A = x * y
A = x * (80 - 2x)
A = 80x - 2x² Agora a área é uma expressão que depende do valor de x.

Para encontrar o ponto máximo da função, pode usar a fórmula do vértice da equação de segundo grau:
Vértice x = -b / 2a
Vértice x = -(80) / 2(-2)
Vértice x = -80 / -4
Vértice x = 20
Ou pode também derivar a área com respeito a x e igualá-la a zero para encontrar o valor de x que maximiza a função:
[tex]\frac{\partial A}{\partial x}=80-4x[/tex]
[tex]80-4x=0[/tex]
[tex]4x=80[/tex]
[tex]x=20[/tex]
No comments:
Post a Comment