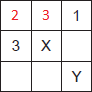
A)

B)

C)

D)

A sequência de letras segue a ordem inversa do alfabeto e vai progressivamente pulando letras.
A sequência de números segue ordem decrescente, o valor subtraído são números ímpares em ordem crescente.

2) (2013 - CETRO) O próximo valor correto para a sequência 0, 6, 24,... é
A) 78.
B) 66.
C) 58.
D) 48.
E) 46.
Questão muito difícil, pois há poucos termos e definir uma regra válida para todos não é fácil.
Acredito que o examinador pretendeu [tex]A_{n}=-3+3^{n}[/tex].
[tex]A_{1}=-3+3^{1}[/tex]
[tex]A_{1}=-3+3=0[/tex]
[tex]A_{2}=-3+3^{2}[/tex]
[tex]A_{2}=-3+9=6[/tex]
[tex]A_{3}=-3+3^{3}[/tex]
[tex]A_{3}=-3+27=24[/tex]
[tex]A_{3}=-3+3^{4}[/tex]
[tex]A_{3}=-3+81=78[/tex]
Nada óbvio.
O pior é que com criatividade é possível chegar a outro resultado. Tome por exemplo, a "função dos divisores", sigma, que associa a cada número natural n a soma de seus divisores naturais elevados à potência k.
[tex]\sigma _{k}(n)=\sum_{d|n}d^{k}[/tex]
[tex]\sigma _{1}(1)=1[/tex] é a soma dos números naturais que dividem 1 elevados à potência 1.
[tex]\sigma _{2}(2)=1^{2}+2^{2}[/tex] é a soma dos divisores de 2 elevados à potência 2.
[tex]\sigma _{1}(3)=1+3[/tex] é a soma dos divisores de 3 elevados à potência 1.
[tex]\sigma _{1}(4)=1+2+4[/tex] é a soma dos divisores de 4 elevados à potência 1.
[tex]\sigma _{3}(6)=1^{3}+2^{3}+3^{3}+6^{3}[/tex] é a soma dos divisores de 6 elevados à potência 3.
Segue que a sequência do enunciado poderia ser definida como:
[tex]A_{n}=\sigma _{3}(n)-\sigma _{1}(n)[/tex]
[tex]A_{1}=\sigma _{3}(1)-\sigma _{1}(1)=1^{3}-1=0[/tex]
[tex]A_{2}=\sigma _{3}(2)-\sigma _{1}(2)=1^{3}+2^{3}-(1+2)=6[/tex]
[tex]A_{3}=\sigma _{3}(3)-\sigma _{1}(3)=1^{3}+3^{3}-(1+3)3=24[/tex]
[tex]A_{4}=\sigma _{3}(4)-\sigma _{1}(4)=1^{3}+2^{3}+4^{3}-(1+2+4)=66[/tex]
Letra B seria a resposta para essa função.
Viagem? Sim, mas é possível, afinal é uma função que gera os três primeiros termos.
3) (2013 - FGV) Em um depósito há apenas bolsas de sangue dos tipos sanguíneos A e O armazenadas em sequência conforme sugerido a seguir:
A2572, A2573, A2574, ..., A2821
O1878, O1879, O1880, ..., O2013
Sabe-se que cada uma das duas sequências segue a ordem dos números naturais sem faltas ou multiplicidades.
A quantidade de bolsas de sangue nesse depósito é
A) 384.
B) 385.
C) 386.
D) 387.
E) 388.
Se você tivesse artigos numerados de 1 a 20, você teria 20 artigos. É fácil contar assim.
Para que a bolsa de sangue A2572 seja a número A1, é necessário subtrair 2571.
2572 - 2571 = 1
2821 - 2571 = 250
Agora as bolsas estão numeradas de A1 a A250.
Faça o mesmo para as bolsas com sangue O.
1878 - 1877 = 1
2013 - 1877 = 136
Agora as bolsas estão numeradas de O1 a O136
Ao todo são 336 bolsas de sangue.
4) (2015 - FCC) Em uma sequência de números inteiros, o primeiro elemento vale 1 e o segundo elemento vale - 1. A partir do terceiro, cada elemento é igual ao produto dos dois elementos imediatamente anteriores a ele. A soma dos primeiros 2015 elementos dessa sequência é igual a
A) -671.
B) -673.
C) -1.
D) -2013.
E) -2015.
O produto é sinônimo de multiplicação entre os elementos.
Os dois primeiros termos são 1 e -1.
A sequência vai seguir o padrão 1, -1, -1, 1, -1, -1, 1, -1, -1, 1, -1, -1, ...
Dá para perceber que um trio de elementos forma um padrão que se repete ao longo da sequência: (1, -1, -1), (1, -1, -1), (1, -1, -1), (1, -1, -1), ...
Em 2015 termos esse padrão vai aparecer 2015/3 = 617 vezes e ainda sobrarão 2 elementos.
O saldo de cada padrão é igual a 1-1-1 = -1.
Portanto, a soma dos 617 padrões é igual a -617.
A soma dos 2 elementos restantes é igual 1-1 = 0.
5) (2014 - VUNESP) As pastas de um arquivo são nomeadas com 4 caracteres alfanuméricos da seguinte maneira:
1.º caractere: uma letra escolhida entre {L, M, N, P, Q, R, S, T, U}
2.º caractere: um algarismo escolhido entre {0, 1, 2, 3, 4, 5}
3.º caractere: uma letra escolhida entre {A, B, C, D, E, F, G, H, J, K, L}
4.º caractere: um algarismo escolhido entre {2, 3, 4, 5, 6, 7}
Cada pasta tem um nome único e todas as pastas estão ordenadas de maneira que a pasta L0A2 é a primeira, L0A3, a segunda, seguindo a ordem alfabética e numérica, até a última pasta, de nome U5L7. Seguindo esse padrão, a pasta de nome R2D2 ocupa a posição
A) 2 000.
B) 2 131.
C) 2 222.
D) 2 323.
E) 2 456.
O jeito é verificar o número de permutações possíveis até chegar em R2D2.
Imagine 4 casas para representar os 4 caracteres. _ * _ * _ * _ A primeira casa contém o primeiro caractere, mas queremos apenas os que antecedem R2D2, então restringimos a primeira casa para começar por uma letra entre {L, M, N, P, Q).
5 * _ * _ * _
A segunda casa pode ser preenchida com qualquer um dos 6 caracteres disponíveis para a segunda posição.
5 * 6 * _ * _
E assim por diante.
Há 5 * 6 * 11 * 6 permutações possíveis, ou seja, 1980 permutações.
Para o primeiro caractere sendo igual a R e o segundo sendo {0, 1} há
1 * 2 * 11 * 6 permutações, isto é, 132.
Para o primeiro caractere sendo igual a R e o segundo sendo 2 e o terceiro sendo igual a {A, B, C} há
1 * 1 * 3 * 6 permutações que é igual a 18
1980 + 132 + 18 = 2130 permutações de L0A1 a R2C7.
A próxima pasta é a R2D2.
6) (2012 - CESGRANRIO)

Na figura mostrada acima, um retângulo de lados 4 cm e 7 cm foi dividido em quadrados cujos lados medem 1 cm. Ao traçar uma diagonal do retângulo observa-se que, ela intercepta os lados de exatamente 10 quadrados, como ressaltado na figura.
Se o retângulo fosse dividido em quadrados de lado medindo 0,5 cm, a diagonal interceptaria os lados de quantos quadrados?
Obs.:Considere que o vértice faz parte do lado do quadrado.
A) 40
B) 22
C) 18
D) 10
E) 5
Se as dimensões dos quadrados passarem de 1 x 1 cm² para 0,5 x 0,5 cm², a grade terá 4 vezes o número de quadrados originais.
A reta atravessará o dobro do número de quadrados anteriores. Porém, no centro, a linha cruzará os quadrados bem no vértice. Portanto os quatro quadrados do centro são interceptados pela reta.
Ao todo são 20 + 2 quadrados interceptados.

7) (2015 - UPENET/IAUPE) Considerando o alfabeto com 26 letras e a regra de formação da sequência abaixo, quais as duas próximas letras que completam a sequência [A E C G E I G K I ...]
A) K O
B) J I
C) G M
D) M K
E) L N
A sequência pode ser dividida em duas listas em ordem alfabética que pulam sempre uma letra:
A _ C _ E _ G _ I _ ?
_ E _ G _ I _ K _ ?
Comepletando os espaços em branco:
A B C D E F G H I J K
D E F G H I J K L M
A primeira letra segue a sequência de baixo e será a letra M.
A segunda letra segue a sequência de cima e será a letra K.
Resposta: letra D.
8) (2012 - IF-SP) Qual é o próximo número da sequência 2, 3, 5, 9, 17,...?
A) 19
B) 33
C) 25
D) 31
E) 29
O valor somado é duplicado em cada termo subsequente. Os valores somados são 1, 2, 4, 8 e 16 ...
2 + 1 = 3
3 + 2 = 5
5 + 4 = 9
9 + 8 = 17
17 + 16 = 33
9) (2012 - Cetro) Assinale a alternativa que substitui corretamente o ponto de interrogação na sequência abaixo.
51, 61, 153, 183, 459, 549, ?
A) 627.
B) 787.
C) 957.
D) 1377.
E) 1647.
ão duas sequências intrelaçadas que seguem a mesma regra de formação. A primeira sequência começa com 51 e a segunda com 61. O próximo termo de cada sequência é três vezes superior ao anterior:
51, __, 153, ___, 459, ___ , ?
__, 61, ___, 183, ___, 549
51 * 3 = 153
153 * 3 = 459
459 * 3 = 1377
10) (2015 - IADES) A sequência numérica (17, 15, 13, ...) foi montada, a partir do segundo termo, somando-se 8 ao algarismo das unidades do termo anterior. Nessas condições, a soma dos algarismos do número que ocupa a 834a posição na sequência é
A) 2.
B) 4.
C) 6.
D) 8.
E) 9.
Pela lógica do enunciado, somente a casa das unidade muda enquanto que a da dezena permanece constante. Os termos vão aparecer de forma cíclica em intervalos de cinco termos.
(17, 15, 13, 11, 19), (17, 15, 13, 11, 19), (17, 15, 13, ...
Ao dividir 834 por 5, obtemos um quociente de 166 e resto igual a 4.
O quociente indica que o ciclo de cinco termos ocorreu de forma completa 166 vezes até o 843º termo.
Após completar o 166º ciclo, restam 4 termos para chegar ao 834º termo. Por isso, o resto 4 significa que o 834º termo é igual ao quarto termo da sequência, 11.
Ao somarmos os dois dígitos do quarto termo da sequência obtém-se 2.
A letra A responde à questão.